Função Quadrática
Definição
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a  0.
0.
Vejamos alguns exemplos de função quadráticas:
Vejamos alguns exemplos de função quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = 1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a  0, é uma curva chamada parábola.
0, é uma curva chamada parábola.
Exemplo:
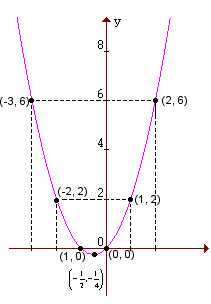
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
|  |
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
se a > 0, a parábola tem a concavidade voltada para cima;
se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a  0, os números reais x tais que f(x) = 0.
0, os números reais x tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
Temos:
Observação
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando 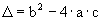 , chamado discriminante, a saber:
, chamado discriminante, a saber:
quando é positivo, há duas raízes reais e distintas;
é positivo, há duas raízes reais e distintas;
quando é zero, há só uma raiz real;
é zero, há só uma raiz real;
quando é negativo, não há raiz real.
é negativo, não há raiz real.
Raízes
As duas raízes da equação quadrática , onde
, onde 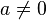 são
são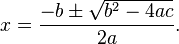 Essa fórmula é chamada de Fórmula de Bhaskara.
Essa fórmula é chamada de Fórmula de Bhaskara.- Dado

- Se
 , então existem duas raízes distintas uma vez que
, então existem duas raízes distintas uma vez que 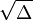 é um número real positivo.
é um número real positivo. - Se
 , então as duas raízes são iguais, uma vez que
, então as duas raízes são iguais, uma vez que 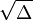 é igual a zero.
é igual a zero. - Se
 , então as duas raízes são números complexos conjugados, uma vez que
, então as duas raízes são números complexos conjugados, uma vez que 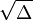 é imaginário.
é imaginário.
Efetuando e
e  ou vice versa, é possível fatorar
ou vice versa, é possível fatorar  como
como  .
.
Formas da função quadráticaUma função quadrática pode ser expressa em três formatos: é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),
é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),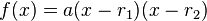 é chamada a forma fatorada, onde r1 e r2 são as raízes da equação quadrática, e
é chamada a forma fatorada, onde r1 e r2 são as raízes da equação quadrática, e é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
Para converter a forma geral para a forma fatorada, é necessário usar a fórmula quadrática e encontrar as raízes r1 and r2. Para converter a forma geral para a forma padrão é necessário usar o processo de completar o quadrado. Para converter a forma fatorada (ou padrão) para a forma geral, é necessário multiplicar, expandir e/ou distribuir os fatores.
GráficoIndependentemente do formato, o gráfico de uma função quadrática é uma parábola (como mostrado abaixo).- Se
 , a parábola abre para cima.
, a parábola abre para cima. - Se
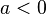 , a parábola abre para baixo.
, a parábola abre para baixo.
O coeficiente a controla a velocidade de aumento (ou decréscimo) da função quadrática a partir do vértice. Números positivos grandes para afazem a imagem de x aumentar mais rápido, fazendo com que a parábola fique mais fechada, mais "magra".O coeficiente b e a, juntos, controlam o eixo de simetria da parábola (e também a coordenada do x do vértice).O coeficiente b sozinho é a declividade da parábola ao cortar o eixo y.O coeficiente c controla a altura da parábola, mais especificamente, é o ponto onde a parábola corta o eixo y.
VérticeO vértice de uma parábola é o número crítico da função quadrática - o ponto onde ela vira, também chamado de turning point. Se a função estiver na forma padrão, o vértice é dado por . Pelo método de completar o quadrado transforma-se a forma geral:
. Pelo método de completar o quadrado transforma-se a forma geral:  emde forma que o vértice da parábola na forma geral sejaSe a função quadrática estiver na forma fatorada
emde forma que o vértice da parábola na forma geral sejaSe a função quadrática estiver na forma fatorada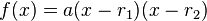 a média aritmética da duas raízes, i.e.,fornece a coordenada x do vértice, e assim o vértice é dado porA linha verticalque passa pelo vértice é chamada de eixo de simetria da parábola.
a média aritmética da duas raízes, i.e.,fornece a coordenada x do vértice, e assim o vértice é dado porA linha verticalque passa pelo vértice é chamada de eixo de simetria da parábola.- Pontos de máximo/mínimo
- O máximo ou mínimo de uma função é sempre obtido no vértice. O seguinte método se baseia na mesma idéia fazendo uso do cálculo. A vantagem desse método é que ele funciona para funções mais gerais.
- Tomando
 como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de
como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de  , se
, se  , tem um ponto mínimo, se
, tem um ponto mínimo, se 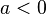 , tem um ponto máximo) é necessário antes encontrar sua derivada:
, tem um ponto máximo) é necessário antes encontrar sua derivada:
- Depois, encontramos as raízes de
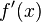 :
:
- Então,
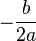 é o
é o  valor de
valor de 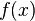 . Agora, para encontrar o valor de
. Agora, para encontrar o valor de 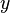 , substituimos
, substituimos 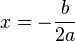 em
em 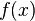 :
:
- Assim, as coordenadas do ponto mínimo/máximo são:
Estudo dos SinaisO estudo dos sinais da função quadrática define os sinais da função para qualquer valor de x. O estudo depende do sinal do coeficiente a e doΔ. Ele é obtido analisando o esboço do gráfico da concavidade da função.- 1º Caso: Δ < 0
Neste caso, a parábola da função não corta o eixo das absissas. Portanto: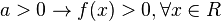
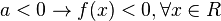
- 2º Caso: Δ = 0Neste caso, a parábola da função corta o eixo das absissas em apenas um ponto. Tem-se duas situações, dependendo o valor do coeficientea e das raízes r1 e r2 (note que r1 < r2):- a > 0

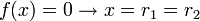
- a < 0
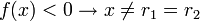
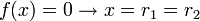
- 3º Caso: Δ > 0Neste caso, a parábola da função corta o eixo das absissas em dois pontos. Novamente, tem-se duas situações, dependendo o valor do coeficiente a (note novamente que r1 < r2):- a > 0


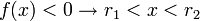
- a < 0
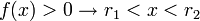

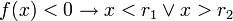
Raiz quadrada de uma função quadráticaA raiz quadrada de uma função quadrática faz surgir ou uma elipse ou uma hipérbole. Se então a equação
então a equação  descreve uma hipérbole. O eixo da hipérbole é determinado pela ordenada do ponto mínimo da parábola correspondente
descreve uma hipérbole. O eixo da hipérbole é determinado pela ordenada do ponto mínimo da parábola correspondente 
Se a ordenada for negativa, então o eixo da hipérbole é horizontal. Se ordenada for positiva, então o eixo da hipérbole é vertical.
Se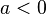 então a equação
então a equação  descreve ou uma elipse ou absolutamente nada. Se a ordenada do ponto máximo da parábola correspondente
descreve ou uma elipse ou absolutamente nada. Se a ordenada do ponto máximo da parábola correspondente  for positiva, então sua raiz quadrada descreve uma elipse, mas a ordenada for negativa ela descreve um conjunto vazio de pontos.
for positiva, então sua raiz quadrada descreve uma elipse, mas a ordenada for negativa ela descreve um conjunto vazio de pontos.
Função quadrática bivariadaUma função quadrática bivariada é um polinômio de segundo grau da formaTal função descreve uma superfície quadrática. Fazendo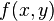 igual a zero, é descrita a intersecção da superfície com o plano
igual a zero, é descrita a intersecção da superfície com o plano  , que é um locus de pontos equivalente a umasecção cônica.
, que é um locus de pontos equivalente a umasecção cônica.
Mínimo/máximoSe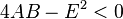 a função não possui máximo ou mínimo e seu gráfico forma um parabolóide hiperbólico.Se
a função não possui máximo ou mínimo e seu gráfico forma um parabolóide hiperbólico.Se a função possui um mínimo se A>0, e um máximo se A<0 e seu gráfico forma um parabolóide elíptico.O mínimo ou máximo de uma função quadrática bivariada é obtido através de
a função possui um mínimo se A>0, e um máximo se A<0 e seu gráfico forma um parabolóide elíptico.O mínimo ou máximo de uma função quadrática bivariada é obtido através de onde:Se
onde:Se e
e  a função não possui máximo ou mínimo e seu gráfico forma um cilindro parabólico.Se
a função não possui máximo ou mínimo e seu gráfico forma um cilindro parabólico.Se e
e 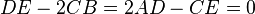 a função alcança o mínimo/máximo em uma linha. Similarmente, um mínimo se A>0 e um máximo se A<0, e seu gráfico forma um cilindro parabólico.
a função alcança o mínimo/máximo em uma linha. Similarmente, um mínimo se A>0 e um máximo se A<0, e seu gráfico forma um cilindro parabólico.
(João vitor) [Bonde Do Estudo](Augusto,Erika M,Jessica,João vitor,Luiz felipe,Wallace e Willian]- Dado

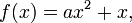


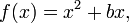



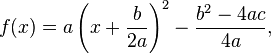








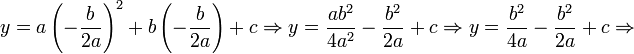
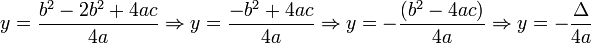


 e nula para
e nula para 



Valeu!!! Agora é só estudar.
ResponderExcluirrenato[chelsea]
ResponderExcluirachei muito interessante os exemplos muito legal.